译者 | 陈峻
审校 | 重楼
自去年以来，诸如ChatGPT 和 Bard之类的大语言模型已将机器学习提升到了一种现象级的地位。开发人员使用它们在辅助编程方面不断探索了从图像生成到疾病检测等领域的应用案例。
鉴于全球各大科技公司都在加大针对机器学习的投入，作为Java开发人员有必要了解如何训练和使用机器学习模型。下面，您将初步了解到机器学习的基本工作原理，有关如何实现和训练机器学习算法的简短指南，以及开发智能应用的最常用监督机器学习方法。
机器学习和人工智能
总的说来，机器学习是从试图模仿人类智慧的AI领域发展而来，使得应用程序能够在无需人工参与的情况下，执行流程改进，并按需更新代码和扩展其功能。
目前，监督学习和无监督学习是两种最流行的机器学习方法。这两种方法都需要向机器输入大量的数据记录，以便其进行关联和学习。而这些被收集到的数据记录通常被称为特征向量。例如，对于某个房屋类数据而言，特征向量可能包括了房屋的总体面积、房间数量、以及房龄等特征。
监督学习
在监督学习中，为了训练算法，机器需要输入一组特征向量和相关标签。其中，标签通常是由人类注释者提供的，代表了对于某个给定问题的正确回答。学习算法会分析特征向量、及其正确标签，以找出它们之间的内部结构和关系。据此，机器就能够学会如何正确地回答问题。
举例来说，一个智能房地产应用为了接受特征向量的训练，人工标注者会根据房屋面积、房间数和房龄等因素，为每套房屋标注出正确的房价。通过对数据进行分析，该房地产应用将会被训练成能够回答“这套房子能卖多少钱？”的问题。
而且在完成训练后，该应用即使碰到未见过的、未标记的特征向量，机器也能够正确地回答新的查询。
无监督学习
在无监督学习中，算法通过编程来预测答案，而无需人工标注，甚至无需提问。无监督学习并非预先确定标签或结果，而是利用海量数据集和处理能力，来发现以前未知的相关性。例如，在消费品的营销过程中，无监督学习可以被用于识别隐藏的关系或消费者分组，以最终形成新的或改进的营销策略。
监督机器学习项目
鉴于所有的机器学习都以数据为基础，因此从本质上讲，算法需要根据源于现实世界的各种数据实例的输入，建立一套数学模型，以最终学会使用新的数据来预测未知的结果。
本文将重点介绍监督学习，这一目前最常见的机器学习方法。让我们延用上文提到的房地产应用案例，用一种有意义的方式为数据贴上标签。在下表 1 中，房屋记录的每一行都包含了一个“房价”标签。通过将行数据与房价标签相关联，算法最终将能够预测不在其数据集中的房屋市场价（注意，房屋面积以平方米为单位，而房价以欧元为单位）。
表 1.房屋记录
特征 | 特征 | 特征 | 标签 |
房屋尺寸 | 房间数量 | 房屋年龄 | 估计费用 |
90平方米/295 英尺 | 2 | 23 年 | 249,000 欧元 |
101平方米/331 英尺 | 3 | 无 | 338,000 欧元 |
1330 平方米/4363 英尺 | 11 | 12 年 | 6,500,000 欧元 |
在早期阶段，您可能需要手工标注数据记录，但最终您将训练应用自动完成该过程。也就是说，标记数据集仅用于训练和测试目的。这一阶段结束后，机器学习模型将能够在无标签数据的实例上工作。例如，您可以向预测算法输入一条新的、无标签的房屋记录，它会根据曾经的训练数据自动预测房价。
训练机器学习模型
监督机器学习的挑战在于，为特定问题找到合适的预测函数。从数学角度讲，我们的挑战就是要找到接收输入变量x，并能够返回预测值的目标预测函数。
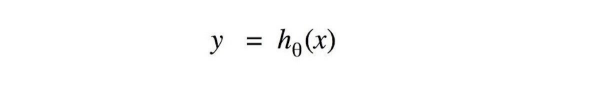图 1.目标预测函数示例
在大多数情况下，x代表了一个多数据点。而在该案例中，它是由房屋尺寸值和房间数量值定义的单个房屋的二维数据点。这些值的数组被称为特征向量。为了预测单个房屋的价格，我们可以使用包含了房屋尺寸和房间数量的特征向量{ 101.0, 3.0 } 去调用目标预测函数：
清单 1.使用特征向量调用目标预测函数
// 目标预测函数 h（学习过程的输出）
Function<Double[], Double> h = ...;
// 设置房屋尺寸=101 和房间数=3 的特征向量
Double[] x = new Double[] { 101.0, 3.0 };
// 并预测房价（标签）
double y = h.apply(x)；在清单 1 中，数组变量x值代表房屋的特征向量。目标预测函数返回的y值是预测的房价。
机器学习面临的挑战是：定义一个尽可能准确地用于未知的、未见过的数据实例的目标预测函数。在机器学习中，目标预测函数（hθ）有时被称为模型。模型是学习过程的结果，也被称为模型训练。
图 2.机器学习模型
学习算法以标注的训练示例为基础，在训练数据中寻找各种结构或模式。在此过程中，学习算法会逐步修改数值以减少损失，从而生成一个能够从数据中进行泛化的模型。
由于机器学习的过程通常是探索性的，因此在大多数情况下，不同的学习算法和配置会被执行多次。当一个模型被确定后，数据也会通过该模型被运行多次。这些迭代也被称为epoch。
最后，算法将根据性能指标对所有模型进行评估，以选出最佳模型，用于计算对于那些未标记数据实例的预测。
线性回归
首先，我们需要选择待使用的学习算法。线性回归是最简单、也是最流行的监督学习算法之一。该算法假定输入特征和输出标签之间存在着线性关系。在图 3 的公式中，通用线性回归函数通过总结特征向量的每个元素，乘以一个theta 参数 (θ) ，以返回预测值。在该训练过程中，θ 参数被用于根据训练数据，来调整回归函数。
图 3.通用线性回归函数
线性回归虽然是一种简单的学习函数，但是它为前馈式神经网络（Forward Neural Network）中使用的梯度下降等更高级形式，奠定了良好的基础。在线性回归函数中，θ 参数和特征参数由订阅数进行枚举。此处的订阅数表示theta 参数 (θ) 和特征参数 (x) 在向量中的位置。需要注意的是，特征x0是一个常数偏移项。为便于计算，其值被设为1。因此，针对特定领域特征（如房屋尺寸）的索引将从x1 开始。如果x1被设置为房屋特征向量的第一个值（房屋尺寸），那么x2将被设置为下一个值（房间数量），以此类推。
注意，在对线性回归进行可视化时，您不妨想象一条在坐标系上的直线，它试图尽可能地接近数据点。下面的清单 2 展示了该线性回归函数的 Java 实现。它在数学上显示为hθ(x)。为了简单起见，该计算使用了double 数据类型。而在apply()方法中，数组的第一个元素已在该函数之外被设置为 1.0。
清单 2.Java 中的线性回归
public class LinearRegressionFunction implements Function<Double[], Double> {
private final double[] thetaVector;
LinearRegressionFunction(double[] thetaVector) {
this.thetaVector = Arrays.copyOf(thetaVector, thetaVector.length);
}
public Double apply(Double[] featureVector) {
// 出于计算原因，第一个元素必须是 1.0
assert featureVector[0] == 1.0;
// simple, sequential implementation
double prediction = 0;
for (int j = 0; j < thetaVector.length; j++) {prediction += thetaVector[j] * featureVector[j];
}
return prediction;
}
public double[] getThetas() {
return Arrays.copyOf(thetaVector, thetaVector.length);
}
}为了创建LinearRegressionFunction 的新实例，我们必须设置 theta 参数。theta 参数或向量被用于使得通用回归函数能够适应基础的训练数据。该代码的 theta 参数将在学习过程中根据训练示例进行调整。显然，训练目标预测函数的质量，只能与给定训练数据的质量相当。
在下一个示例中，我们对LinearRegressionFunction进行实例化，以根据房屋尺寸预测房价。考虑到x0必须是 1.0 的常量，目标预测函数将使用两个 theta 参数进行实例化。而theta 参数则是学习过程的输出。在创建了新的实例后，面积为 1330 平方米的房屋价格预测结果如下：
// 这里使用的 Theta 向量是训练过程的输出
double[] thetaVector = new double[] { 1.004579, 5.286822 };
LinearRegressionFunction targetFunction = new LinearRegressionFunction(thetaVector);
// create the feature vector function with x0=1 (for computational reasons) and x1=house-size
Double[] featureVector = new Double[] { 1.0, 1330.0 };
// 进行预测
double predictedPrice = targetFunction.apply(featureVector)；目标预测函数的预测线在图 4 中显示为一条蓝线。这条线是通过对所有房屋面积值进行目标预测计算得出的。同时，图中还包括了用于训练的“价格-尺寸”对。
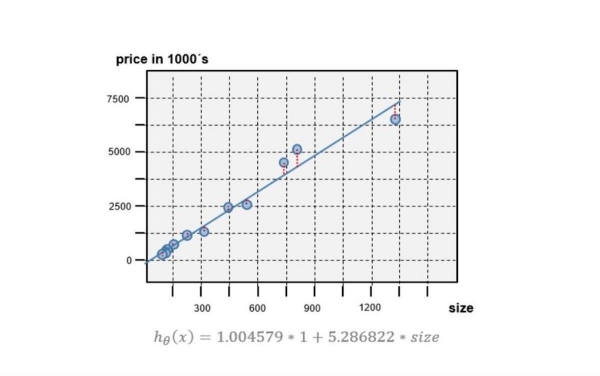图 4 目标预测函数预测线
上图坐标的截距和斜率是由θ 向量{ 1.004579, 5.286822 } 定义。该预测图看似十分贴切，但是我们又怎么知道该 Theta 向量一定适合自己的应用呢？如果改变第一个或第二个 theta 参数，函数的适合度会更好吗？为了确定最合适的 theta 参数向量，我们需要一个实用函数（Utility Function）来评估目标预测函数的性能。
目标预测函数的评估
在机器学习中，成本函数（J(θ)）（又称“损失函数”）通常被用于计算给定目标预测函数的平均误差或“成本”。图 5 显示了一个函数例子。
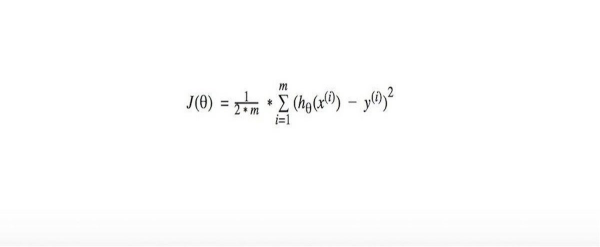图 5 成本函数
成本函数表示模型与训练数据的适合程度。若要确定训练目标预测函数的成本，我们可以计算每个房屋示例(i) 的平方误差。此处的误差是计算得出的y值，与房屋示例i 的实际y值之间的距离。例如，面积为 1330 平方米的房屋的实际价格为 6,500,000 欧元，而经过训练的目标预测函数预测的房屋价格为 7,032,478 欧元，其差距（或误差）为 532,478 欧元。您可以在图 4中找到这一差距。图中的差距（或误差）是以垂直红色虚线的形式，显示在每个训练“价格-尺寸”对中。
要计算经过训练的目标预测函数的成本，我们必须总结示例中每栋房屋的平方误差，并计算出平均值。只有J(θ) 的成本值越小，目标预测函数的预测才越精确。
在下面的代码列表中，代价函数的简单 Java 实现将目标预测函数、训练记录列表、及其相关标签作为输入。预测值将在循环中被计算，而误差则通过减去真实标签值来计算。据此，它将汇总平方误差并计算平均误差。成本也将以双值的形式返回：
public static double cost(Function<Double[], Double> targetFunction,
List<Double[]> dataset,
List<Double> labels) {
int m = dataset.size();
double sumSquaredErrors = 0;
// 计算每个训练示例的平方误差（“差距”），并将其与总和相加
for (int i = 0; i < m; i++) {
// 获取当前示例的特征向量
Double[] featureVector = dataset.get(i);
// 根据真实值（标签）预测值并计算误差
double predicted = targetFunction.apply(featureVector);
double label = labels.get(i); double gap = targetFunction.ap ply(f eat ureVector); double label = labels.get(i);doublegap= targetFunction.apply(featureVector).get(i);
double gap = predicted - label;sumSquaredErrors += Math.pow(gap, 2);
}
// 计算并返回误差的平均值（越小越好）
return (1.0 / (2 * m)) * sumSquaredErrors;
}用梯度下降法训练目标预测函数
虽然代价函数有助于分别评估目标预测函数和 theta 参数的质量，但仍需要计算最佳适合的 theta 参数。在此，我们可以使用梯度下降算法来进行计算。
用梯度下降法计算 theta 参数
梯度下降法能够使得成本函数最小化。也就是说，它能够根据训练数据找到产生最低成本（J(θ)）的 Theta 组合。 梯度下降法通过使用部分导数，逐步调整每个变量来实现这一点。 这是反向传播的一种典型形式，而所有其他形式都会基于该形式。
图 6 显示了一种简化算法，可用于计算新的、适合度更高的 Thetas：
图 6.梯度下降使得成本函数最小化
在每次迭代中， Theta向量的每个参数 θ 都会计算出一个新的、更好的值。同时，学习率α持续控制着每次迭代的计算步长。这种计算将会重复进行，直到得到一个适合且够好的 θ 值组合。例如，图 7 中的线性回归函数就有三个 theta 参数：
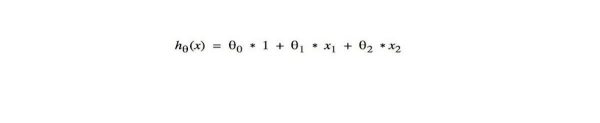图 7.带有三个theta 参数的线性回归函数
在每次迭代（"epoch"）中，算法都会并行地计算出每个 theta 参数的新值：θ0、θ1 和θ2。而每次迭代后，您都可以使用新的 Theta 向量{θ0,θ1,θ2} 再创建一个新的、适合度更高的LinearRegressionFunction实例。
清单 3 显示了梯度下降算法的 Java 代码。回归函数的各个 theta 将使用训练数据、数据标签和学习率(α)来进行训练。函数的输出则使用由新的 theta 参数改进后的目标预测函数。其中，train()方法将会被反复调用，并输入新的目标预测函数与上一次计算，得出的新 theta。这些调用都会重复进行，直到调整后的目标预测函数的成本达到最低点。
清单 3.Java 中的梯度下降算法示例
public static LinearRegressionFunction train(LinearRegressionFunction targetFunction,
List<Double[]> dataset,
List<Double> labels,
double alpha) {
int m = dataset.size();
double[] thetaVector = targetFunction.getThetas();
double[] newThetaVector = new double[thetaVector.length];
// 计算 theta 数组中每个元素的新 theta
for (int j = 0; j < thetaVector.length; j++) {
// 总结误差差距 * 特征
double sumErrors = 0;
for (int i = 0; i < m; i++) {
Double[] featureVector = dataset.get(i);
double error = targetFunction.apply(featureVector) - labels.get(i);sumErrors += error * featureVector[j];
}
// 计算新的 theta 值
double gradient = (1.0 / m) * sumErrors;newThetaVector[j] = thetaVector[j] - alpha * gradient;
}
returnnew LinearRegressionFunction(newThetaVector);
}若要验证成本是否持续下降，我们可以在每个训练步骤后执行成本函数J(θ)。其预期结果是，每迭代一次，成本就必须降低一次。如果没有减少的话，则说明学习率参数值过大，算法超过了最小值。那么在这种情况下，梯度下降算法就会失效。
为什么这种模式行不通
图 8 显示了使用计算出的新theta 参数的目标预测函数。其初始 Theta 向量为{ 1.0, 1.0 }。左侧一列显示的是迭代了 50 次后的预测图；中间一列显示的是迭代了 200 次后的预测图；而右侧一列显示的是迭代了 1000 次后的预测图。如图所示，随着新目标预测函数的适合效果越来越好，每次迭代后的成本都在降低。迭代 500 到 600 次后，θ 参数不再发生显著变化，成本也就达到了稳定的高点。此时，目标预测函数的精度将不再显著提高。
图 8.成本随着每次迭代而降低
虽然经过 500 到 600 次迭代后，成本不再显著降低，但是目标预测函数似乎仍然不是最优的。在机器学习中，我们常用“欠适合（Underfitting）”一词用来表示学习算法没有捕捉到数据的潜在趋势。
根据生活中的实际经验，对于面积大的房产，其每平方米的预计价格会逐渐下降。据此，我们可以得出结论：该训练过程中使用到的模型，即目标预测函数，并没能很好地适合真实数据。鉴于“欠适合”通常是由于模型过于简单造成的，那么在本案例中，是由于我们的简单目标预测函数仅使用了单一的房屋尺寸特征所造成。显然，仅凭这些数据是不足以准确地预测房屋成本的。
添加和扩展特征
如果您发现目标预测函数不适合待解决的问题，一种常见的纠偏方法是，通过在特征向量中添加更多的特征来对其进行调整。例如，在前面的房屋价格示例中，您可以添加诸如：房间数量或房龄等更多房屋特征。同时，您也可以使用一个多值特征向量，如：{ 大小、房间数、房龄 }，来描述房屋实例，而不仅仅使用{ 大小}，这个单一的特定领域特征向量。
当然，在某些情况下，可用的训练数据集中并没有足够的特征。那么您可以尝试着添加由现有特征计算得出的多项式特征。例如，您可以扩展房价目标预测函数，使其包含计算出的平方尺寸特征 (x2)：
图 9.利用多项式特征扩展的目标预测函数
值得注意的是，在使用多个特征时，我们需要进行特征的扩展（或“归一化”），以规范不同特征的范围。例如，size2特征的取值范围就比 size 特征的取值范围大一个量级。如果不对特征进行扩展，size2特征将主导整个成本函数。而size2特征所产生的误差值将远高于仅由尺寸特征产生的误差值。下图 10 显示了一种简单的特征扩展算法。
图 10.简单的特征扩展算法
该算法由如下Java 代码清单中的FeaturesScaling类实现。FeaturesScaling类提供了一个工厂方法（Factory Method），可用于创建根据训练数据调整的扩展函数。在内部，训练数据的实例被用来计算平均值、最小值和最大值常数。而由此产生的函数会使用一个特征向量，并生成一个带有扩展特征的新特征向量。如下图所示，训练过程和预测调用都需要对特征进行扩展：
// 创建数据集
List<Double[]> dataset = new ArrayList<>();dataset.add(new Double[] { 1.0, 90.0, 8100.0 }); // 房屋#1 的特征向量dataset.add(new Double[] { 1.0, 101.0, 10201.0 }); // 房屋#2 的特征向量dataset.add(new Double[] { 1.0, 103.0, 10609.0 }); // ...
//....
// 创建标签
List<Double> labels = new ArrayList<>();labels.add(249.0); // 房屋#1的价格标签labels.add(338.0); // 房屋#2的价格标签labels.add(304.0); // ...
//...
// 扩展特征列表
Function<Double[], Double[]> scalingFunc = FeaturesScaling.createFunction(dataset);
List<Double[] > scaledDataset = dataset.stream().map(scalingFunc).collect(Collectors.toList());
// 使用初始值创建假设函数，并以 0.1 的学习率对其进行训练
LinearRegressionFunction targetFunction = new LinearRegressionFunction(new double[] { 1.0, 1.0, 1.0 });
for (int i = 0; i < 10000; i++) {targetFunction = Learner.train(targetFunction, scaledDataset, labels, 0.1);
}
// 对面积为 600 m2 的房屋进行预测
Double[] scaledFeatureVector= scalingFunc.apply(new Double[] { 1.0, 600.0, 360000.0 });
double predictedPrice = targetFunction.apply(scaledFeatureVector)；随着更多的特征被添加，您可能会发现目标预测函数也适合得越来越好。不过值得注意的是，如果添加了太多的特征，则最终可能会导致目标预测函数出现过度适合（Overfitting）。
过度适合和交叉验证
当目标预测函数或模型与训练数据适合得好过头时，就会出现过度适合。而过度适合的模型则会捕捉到训练数据中的噪声或随机波动。图 11 中最右侧的图表显示了一种过度适合的行为模式。
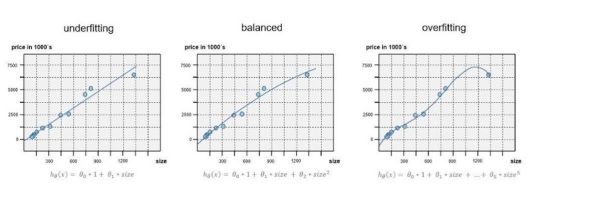图 11.具有过度适合行为的目标预测函数示例
虽然过度适合模型在训练数据上非常匹配，但当需要求解未知的、未见过的数据时，它的表现会相当糟糕。目前，我们有如下三种方法可以避免过度适合：
- 使用更大的训练数据集。
- 通过增加正则化，来改进机器学习算法。
- 如上面的中间图表所示，减少特征的使用。
如果您的预测模型出现过度适合的话，则应该删除任何对其准确性无益的特征。此处的挑战在于，如何找到对于预测结果贡献最大的特征。
如上图所示，过度适合可以通过可视化图形来识别。尽管这种方法在使用二维或三维图形时效果很好，但是如果使用两个以上的特定域特征，则会变得相当困难。因此，交叉验证经常被用来检测过度适合。
在交叉验证中，一旦学习过程结束，我们便可使用未见过的验证数据集，对训练好的模型进行评估。通常，我们可以将可用的标注数据集分为三个部分：
- 训练数据集。
- 验证数据集。
- 测试数据集。
在上述案例中，60% 的房屋示例记录可用于训练目标算法的不同变体。一旦学习过程结束，剩余的一半未接触过的示例记录，将被用于验证训练过的目标算法，是否能够很好地处理未见过的数据。
通常情况下，我们会先选择一种最合适的目标算法。而另一半未经处理的示例数据将用于计算最终选定模型的误差指标。当然，这种技术也有其他的变种，比如：k 折交叉验证等。此处就不展开了。
小结
在上文中，我们在了解机器学习相关概念的基础上，介绍了一个监督学习的示例，并使用梯度下降算法来训练目标预测函数。同时，我们也讨论了一种模型的欠适合示例，以及如何通过添加和扩展特征来实现纠偏。最后，我们还简要介绍了过度适合的危险性，以及如何对其予以纠正。
译者介绍
陈峻（Julian Chen），51CTO社区编辑，具有十多年的IT项目实施经验，善于对内外部资源与风险实施管控，专注传播网络与信息安全知识与经验。
原文标题：Machine learning for Java developers: Algorithms for machine learning，作者：Gregor Roth和Matthew Tyson
发表评论 取消回复